INFORMÁTICA

SISTEMAS DE NUMERACIÓN

Un sistema de numeración es un conjunto de símbolos y reglas de generación que permiten construir todos los números válidos.

Un sistema de numeración puede representarse como

donde:

•  es el sistema de numeración considerado (p.ej. decimal, binario, etc.).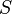
•  es el conjunto de símbolos permitidos en el sistema. En el caso del sistema decimal son {0,1,...9}; en el binario son {0,1}; en el octal son {0,1,...7}; en el hexadecimal son {0,1,...9,A,B,C,D,E,F}.
•  son las reglas que nos indican qué números son válidos en el sistema, y cuáles no. En un sistema de numeración posicional las reglas son bastante simples, mientras que la numeración romana requiere reglas algo más elaboradas.

Estas reglas son diferentes para cada sistema de numeración considerado, pero una regla común a todos es que para construir números válidos en un sistema de numeración determinado sólo se pueden utilizar los símbolos permitidos en ese sistema.

Para indicar en qué sistema de numeración se representa una cantidad se añade como subíndice a la derecha el número de símbolos que se pueden representar en dicho sistema.

Al igual que otras civilizaciones mesoamericanas, los mayas utilizaban un sistema de numeración de raíz mixta de base 20 (vigesimal). También los mayas pre-clásicos desarrollaron independientemente el concepto de cero alrededor del año 36 a.c.
Este es el primer uso documentado del cero en América, aunque con algunas peculiaridades que le privaron de posibilidad operatoria. Las inscripciones, los muestran en ocasiones trabajando con sumas de hasta cientos de millones y fechas tan extensas que tomaba varias líneas el poder representarlas.

CLASIFICACION:

Los sistemas de numeración pueden clasificarse en dos grandes grupos: posicionales y no-posicionales:

• En los sistemas no-posicionales los dígitos tienen el valor del símbolo utilizado, que no depende de la posición (columna) que ocupan en el número.
• En los sistemas de numeración ponderados o posicionales el valor de un dígito depende tanto del símbolo utilizado, como de la posición que ése símbolo ocupa en el número.

Por ejemplo, el sistema de numeración egipcio es no posicional, en cambio el babilónico es posicional. Las lenguas naturales poseen sistemas de numeración posicionales basados en base 10 ó 20, a veces con subsistemas de cinco elementos. Además, en algunas pocas lenguas los numerales básicos a partir de cuatro tienen nombres basados en numerales más pequeños

(http://es.wikipedia.org/wiki/Sistema_de_numeración)


EJEMPLOS DE SISTEMAS DE NUMERACIÓN:

• Base64
• Numeración Egipcia
• Numeración Maya
• Numeración Romana
• Sistema Alfanumérico
• Sistema Binario
• Sistema de Numeración Decimal
• Sistema Duodecimal
• Sistema Hexadecimal
• Sistema Octal

El siguiente vídeo es una forma amena de comprender la evolución de un sistema numérico.

Obsérvala con atención para que posteriormente desarrolles el taller.

"LA HISTORIA DEL NUMERO 1"

_____________________________________

EN CONSTRUCCIÓN...